Funktion und Aufbau einer PEMFC

PEMFC ist die englische Abkürzung für "proton exchange membrane fuel cell", zu deutsch Protonenaustauschmembran-Brennstoffzelle. Dieser Brennstoffzellen-Typ wird oft auch mit PEFC (polymer electrolyte fuel cell) abgekürzt, und PEM kann auch für Polymerelektrolytmembran stehen.

Inhaltsverzeichnis

I. Funktion einer Brennstoffzelle (allgemein)
II. Aufbau einer PEM-Einzelzelle
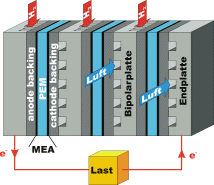
III. Der PEMFC-Stack
IV. Eigenschaften der PEMFC

I. Funktion einer Brennstoffzelle (allgemein)

In einer Brennstoffzelle (BZ) erfolgt eine kontrollierte Oxidation des in der Regel gasförmigen Brennstoffs, meist Wasserstoff, mit Sauerstoff oder Luft. Der wichtigste Unterschied zur bekannten Knallgasreaktion (H₂ + 1/2 O₂ → H₂O), bei der Wasserstoff mit Sauerstoff unter heftiger Explosion zu Wasser reagieren, ist der, dass die Oxidation des Wasserstoffs und die Reduktion des Sauerstoffs durch einen Elektrolyten räumlich voneinander getrennt sind.

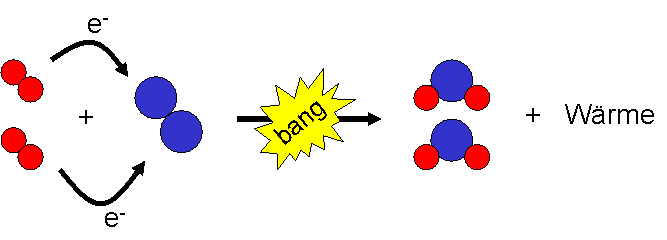
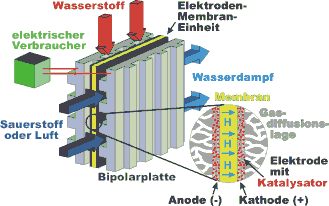
Durch diese Trennung findet kein direkter Elektronentransfer vom Wasserstoff zum Sauerstoff (wie in der Knallgasreaktion), sondern ein indirekter Elektronentransfer statt. Die Elektronen werden über zwei Elektroden am Elektrolyten (hier gelb dargestellt) "vorbeigeleitet". Auf diese Weise kann ein Teil der im Wasserstoff gespeicherten chemischen Energie als elektrische Energie genutzt werden. Der Ladungsausgleich erfolgt durch einen Ionentransport (hier Protonentransport) durch den Elektrolyten.

Das Kernstück einer jeden BZ ist der Elektrolyt. Deshalb werden die einzelnen BZ-Typen auch nach der Art der verwendeten Elektrolyten unterschieden. In der PEMFC besteht der Elektrolyt aus einer protonenleitenden Membran. Auf der Membran sind die beiden Elektroden (Anode und Kathode) aufgebracht. An der Anode wird Wasserstoff durch einen geeigneten Edelmetall-Katalysator (z. B. Pt) zu Protonen oxidiert (engl.: hydrogen oxidation reaction, HOR) und gibt jeweils sein Elektron ab:

H₂ → 2 H⁺ + 2 e^-

Die Anode bildet den Minus-Pol einer Zelle, da hier die Elektronen aus dem System ausgeführt werden. Die Protonen wandern von der Anode durch die Membran (zum Beispiel einem Polymer aus Poly-perfluorsulfonsäure) zur Kathode. An der Katode, dem Plus-Pol, werden die Elektronen wieder dem System zugeführt. Dadurch diese Elektronen wird der an der Kathode bereitgestellte Sauerstoff reduziert (engl.: oxygen reduction reaction, ORR) und nimmt die durch den Elektrolyten gewanderten Protonen auf. Bei dieser Reaktion entsteht das Produktwasser.

1/2 O₂ + 2 e^- + 2 H⁺ → H₂O

Die Gesamtreaktion einer H₂/O₂-BZ lautet demnach:

H₂ + 1/2 O₂ → H₂O

Ganz allgemein erfolgt der für den Ablauf der chemischen Reaktion in der Brennstoffzelle notwendige Ladungsausgleich durch die Wanderung von Ionen durch den Elektrolyten. Je nach BZ-Typ kann der Elektrolyt sauren oder basischen Charakter haben. In sauren Elektrolyten erfolgt der Ladungsausgleich durch die Wanderung von Protonen und in basischen Elektrolyten durch Wanderung von Oxidionen (oder gebunden in Carbonationen).

I. 2. Volumenstrom, Gasumsatz und Stöchiometrie

Nach dem Faraday´chen Gesetz (n = Q/zF) lässt sich der Gasbedarf einer Einzelzelle als Molenstrom φ_mol berechnen:

φ_mol = 1 / zF [φ_mol] = mol/ As

Dabei ist F die Faraday-Konstante (F = 96485,3 As/mol) und z die Anzahl der ausgetauschten Elektronen (z = 2 bei obiger Reaktion). Sinnvoller als die molare Größe ist die Angabe als Volumenstrom φ in Normliter pro Ampere und Minute (Nl/A min). Die Umrechnung erfolgt über das Molvolumen eines idealen Gases (V_mol = V/n = RT/p = 22,414 Nl/mol) unter Normbedingungen (101325 Pa, 0°C oder 273,15K).

φ = φ _mol · V_mol · 60s/min [φ] = Nl/ A min

Durch die Umrechnung in Volumenströme werden diese Berechnungen abhängig von Druck und Temperatur. Die auf Normbedingungen (s. o.) bezogenen Volumenströme müssen deswegen in Normlitern angegeben werden (engl.: standard liter per minute, slpm).

Durch Einsetzen erhält man folgende Werte für Wasserstoff und Sauerstoff pro Einzelzelle:

φ_H2 = 7,0·10^-3 Nl/A min   und   φ _O2 = 3,5·10^-3 Nl/A min

Wenn die BZ mit Luft an Stelle von reinem Sauerstoff betrieben wird, muss durch den Molenbruch (x = 0,21) geteilt werden, da 21 Vol.% Sauerstoff in Luft enthalten sind:

φ_Luft = 16,6·10^-3 Nl/A min.

Dieser theoretische Gasbedarf für Anode und Kathode entspricht einer Stöchiometrie von λ = 1 bzw. einem 100%igen Gasumsatz u. Dabei gilt folgender Zusammenhang zwischen dem Umsatz u und der Stöchiometrie λ:

λ = 1/u

In der Praxis ist der Umsatz immer kleiner als 100% (u < 100%) bzw. die Stöchiometrie größer als eins (λ > 1), da die BZ die bereitgestellten Reaktionsgase nie vollständig umsetzen kann. Das bedeutet, dass mehr Wasserstoff bzw. Sauerstoff oder Luft für den Betrieb einer Zelle bereitgestellt werden müssen als der Theorie nach berechnet. Wenn doppelt so viel Gas bereitgestellt wird, entspricht das einem Umsatz von u = 50% oder einer Stöchiometrie von λ = 2. Der für den Betrieb einer Einzelzelle notwendige Gasbedarf im H ₂/Luft-Betrieb berechnet sich deshalb nach folgender Formel:

Anode: φ_H2 = λ_anode · 7,0·10^-3 Nl/A min
Kathode: φ_Luft = λ_cathode · 16,6·10^-3 Nl/A min

Die Stöchiometrie, mit der ein BZ-Stack betrieben werden kann, ist von vielen Faktoren abhängig (Gaszusammensetzung, Flowfield, Wassermanagement, ...). Um in einem BZ-System einen guten Wirkungsgrad (siehe unten) zu erreichen, muss auf der Anodenseite eine möglichst niedrige Stöchiometrie (hoher Umsatz) an Wasserstoff gefahren werden. Dabei wird zwischen Bruttoumsatz und Single-Pass-Umsatz unterschieden. Der Bruttoumsatz ist der Umsatz, der sich auf das BZ-System bezieht. Der Single-Pass-Umsatz dagegen bezieht sich auf den BZ-Stack. Wenn das BZ-System mit einer Anodenumwälzung (Anodenrezirkulation) betrieben wird, können Brutto- und Single-Pass-Umsatz verschieden sein. Mehr dazu unter BZ-System. Realistisch sind Werte λ_anode ≤ 1,5 (Single-Pass-Umsatz). Die Stöchiometrie auf der Kathodenseite liegt beim Luftbetrieb oft zwischen 1,5 ≤ λ_cathode ≤ 4.

I. 3. Thermodynamik der Brennstoffzelle

Die maximale Arbeit, die von einem System geleistet werden kann, ist durch die freie Gibbs´ Enthalpie ΔG gegeben. Wenn Temperatur und Druck konstant sind (∂T = 0 und ∂p = 0), dann kann bei einer elektrochemischen Reaktion die maximale Arbeit als elektrische Spannung genutzt werden. Diese Spannung nennt man Elektromotorische Kraft (EMK) , Gleichgewichtspannung oder Ruhespannung. Entsprechend dem Potential der obigen Reaktion berechnet sich die Einzelzellspannung U_EZ,0 der H₂/O₂-BZ wie folgt:

U_{EZ, 0} = -ΔG / zF

Dabei ist F die Faraday-Konstante (F = 96485,3 As/mol) und z die Zahl der ausgetauschten Elektronen (hier z = 2).

Für die weiteren Betrachtungen muss nun zwischen dem Brennwert (früher oberer Heizwert, englisch upper heating value UHV) und dem Heizwert (früher unterer Heizwert, englisch lower heating value LHV) von Wasserstoff unterschieden werden. Der Brennwert liegt dabei immer über dem Heizwert. Der Brennwert bzw. Heizwert eines Brennstoffes entspricht der Reaktionsenthalpie ΔH_R der chemischen Reaktion, bei der der Brennstoff mit Sauerstoff oxidiert wird und Wasser entsteht. Fällt dieses Produktwasser flüssig an, spricht man vom Brennwert ΔH_o des Brennstoffs. Wenn das Produktwasser gasförmig anfällt, spricht man vom Heizwert ΔH_u. Der Betrag von ΔH_o ist um den Betrag der Verdampfungsenthalpie des Wassers ΔH_verd größer als |ΔH_u|.

Für Wasserstoff und damit für die H₂/O₂-BZ bedeutet das bei Standardbedingungen (25°C, 1 bar):

Heizwert: H₂ + 1/2 O₂ → H₂O_(g) ΔH_u = -241,82 kJ/mol (mit ΔG_u = -228,57 kJ/mol)

bzw.

Brennwert: H₂ + 1/2 O₂ → H₂O_(l) ΔH_o = -285,83 kJ/mol (mit ΔG_o = -237,41 kJ/mol)

Aus diesem Grund ist es wichtig, bei allen weiteren Betrachtungen immer den Bezug auf den Brenn- oder Heizwert anzugeben.

Die maximale, theoretische Zellspannung oder EMK der H₂/O₂-BZ beträgt damit nach obiger Gleichung U_EZ,0 = 1,229V (bezogen auf ΔH_o) und U_EZ,0 = 1,184V (bezogen auf ΔH_u).

Den Zusammenhang zwischen ΔH und ΔG beschreibt die Gibbs-Helmholtz-Gleichung

ΔG = ΔH - TΔS.

Da bei der chemischen Reaktion in der H₂/O₂-BZ ΔS negativ ist, obige Reaktion aber spontan abläuft, muss der Entropieterm TΔS in Form von Wärme (thermischer Energie) an die Umgebung abgeführt werden. Der Entropietherm wird auch als reversible Wärmetönung bezeichnet. Dieser Teil der chemischen Energie, der (laut Thermodynamik) nicht in Arbeit und damit auch nicht in elektrische Energie umgewandelt werden kann, fällt also in Form von Wärme bei der BZ-Reaktion an.

Aus der Gibbs-Helmholtz-Gleichung ergibt sich eine lineare Abnahme der Einzelzellspannung mit zunehmender Temperatur (In einem kleinen Temperaturbereich können ΔG, ΔH und ΔS als temperaturunabhängig betrachtet werden!). Bei 800°C beträgt die Zellspannung nur noch U_EZ,0 = 1,046V (bezogen auf ΔH _u).

I. 4. Kinetik der Brennstoffzelle

Die bisherige thermodynamische Betrachtung gilt nur, solange sich das System im Gleichgewicht befindet. Sobald der Stromkreis mit einer BZ und einem elektrischen Verbraucher geschlossen wird, fließt ein Strom und es treten elektrische Verluste in Form von Überspannungen (elektrochemische "Reibung") auf. Diese Überspannungen verringern die Spannung der BZ, und zwar zum so stärker, je höher die Stromstärke I (bzw. Stromdichte j) ist. Die Stromdichte berechnet sich aus der Stromstärke I und der aktiven Elektrodenfläche A:

j = I / A [j] = A/cm²

Überspannungen sind das Ergebnis von kinetisch gehinderten Elektrodenreaktionen und führen zu mehr oder weniger hohen Verlusten. Zusätzlich zu den Entropieverlusten (s. o.) wird durch Überspannungen ein Teil der chemischen Energie als Wärme abgegeben und kann dadurch nicht mehr als elektrischer Energie genutzt werden.

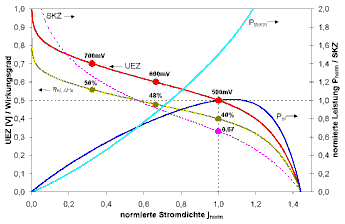
Einige Überspannungen zeigen ein nichtlineares Verhalten. Dadurch ergibt sich ein typischer Kurvenverlauf für die Strom-Spannungs-Kennlinie (englisch polarization curve oder PolCurve) einer BZ. Bei dieser Kennlinie wird die Einzelzellspannung U_EZ(j) (Klemmspannung) in Abhängigkeit der Stromdichte j aufgezeichnet. In der nächsten Abbildung ist der typische Verlauf einer solchen U-I-Kennlinie dargestellt (rote Kurve). Die offene Zellspannung (open cell voltage, OCV) ist die Leerlaufspannung einer BZ, also diejenige Einzelzellspannung, die ohne Stromfluss gemessen wird. In der Praxis werden Werte zwischen 950 und 1000mV gemessen. Warum ist die OCV niedriger als die EMK? Die Ursache liegt in der sogenannten Ruhepolarisation, die unter anderem verursacht wird durch
a) Mischpotential im H₂O₂-Pfad (E₀ = 0,67V),
b) Bildung von Platinoxid bei Potentialen > 0,8V,
c) Diffusion von H₂ durch Membran.

Die nebenstehende Abbildung zeigt den typischen Verlauf einer U-I-Kennlinie (rote Kurve). Die Stromdichte ist hier normiert auf den Punkt maximaler elektrischer Leistung (dunkelblaue Kurve). Weiterhin sind die thermische Leistung (hellblaue Kurve), der elektrische Wirkungsgrad (grüne Kurve) und die Stromkennzahl (gestrichelte Linie) eingezeichnet. Alle Angaben beziehen sich auf den Heizwert von Wasserstoff. Die U-I-Kennlinie fällt zuerst bei kleinen Stromdichten stark ab. Dieser große Spannungsabfall bei sehr kleinen und kleinen Stromdichten wird durch die Überspannung der Sauerstoffreduktionsreaktion (englisch oxygen reduction reaction ORR) verursacht. Im Bereich mittlerer Stromdichte gibt es einen annähernd linearen Zusammenhang zwischen Strom und Spannung, der durch den inneren Widerstand der BZ verursacht wird. Bei hohen Stromdichten wird die Reaktionskinetik durch Diffusion begrenzt, hier fällt die Zellspannung schnell ab und geht gegen Null.

Anmerkung: In der dargestellten U-I-Kennlinie ist die Stromdichte normiert auf den Punkt maximaler elektrischer Leistung bei einer Einzelzellspannung von etwa U_EZ(j) = 0,5V. Ebenso ist die elektrische Leistung auf diesem Punkt normiert.

I. 5. Wirkungsgrade der Brennstoffzelle

Weitere Wirkungsgrade (Betriebs- und Gesamtwirkungsgrad) siehe Brennstoffzellensysteme.

I. 6. Elektrische und thermische Leistung einer Brennstoffzelle

Für die elektrische Leistung einer BZ gilt:

P_el = U_EZ(j) · I

Dabei ist U_EZ die Einzelzellspannung und I die Stromstärke.

Neben elektrischer Energie (Strom) liefert die BZ auch thermische Energie (Wärme). Diese thermische Energie setzt sich aus zwei Teilen zusammen, einem reversiblen und einem irreversiblen. Der reversible Teil ist der Entropieterm TΔS, der irreversible Teil entsteht durch Überspannungsverluste. Der Teil der gesamten chemischen Energie des Brennstoffs, der nicht in Strom umgewandelt werden kann, fällt in Form von Wärme an.

Die thermische Leistung einer BZ kann aus der Einzelzellspannung U_EZ(j) und der Stromstärke berechnet werden. Um die Gleichung zu vereinfachen, geht man von einer hypothetischen auf ΔH_u bezogenen Spannung (ΔH_u/zF = 1,253 V) aus und berechnet daraus die gesamte (elektrische plus thermische) Leistung:

P_ges = 1,253 V · I

Die thermische Leistung ist die (chemische) Gesamtleistung minus der elektrischen Leistung:

P_therm = P_ges - P_el = (1,253 V - U_EZ(j)) · I

In obiger Abbildung ist sowohl die elektrische Leistung (dunkelblaue Kurve) als auch die thermische Leistung (hellblaue Kurve) dargestellt. Man erkennt gut, dass die elektrische Leistung ihr Maximum in der Nähe einer Einzelzellspannung von U_EZ(j) = 500mV besitzt. Die thermische Leistung ist in diesem Punkt bereits mehr aus doppelt so groß wie die elektrische Leistung.

Wenn zusätzlich zur elektrischen Leistung auch die thermische Leistung einer BZ genutzt wird, können in der Praxis Gesamtwirkungsgrade um die 80% erreicht werden!

Die Verschiebung der U-I-Kennlinie hin zu hohen Stromdichten ist das Ziel der Forschung. Dazu müssen die Überspannungen bei hohen Stromdichten minimiert werden. Je höer die Stromdichte bei einer bestimmten Einzelzellspannung ist, desto besser arbeitet eine BZ und desto höher ist der elektrisch Wirkungsgrad und die elektrische Leistung.

II. Aufbau einer PEM-Einzelzelle

Die nebenstehende Abbildung zeigt den schematischen Aufbau einer einzelnen PEM-Brennstoffzelle. Die Membran ist eine dünne Folie (30 bis 170 μ), auf der auf beiden Seiten Elektroden mit einem Katalysator aufgebracht ist. Als Katalysator dienen fein verteilte Edelmetalle auf Kohle, meist Pt auf der Kathodenseite und Pt/Ru auf der Anodenseite. Die Katalysatorbelegung ist kleiner als 0,5 mg/cm2. Die Membran mit den beidseitigen Elektroden wird als Elektrode-Membran-Einheit (EME), MEA (membrane electrode assembly) oder CCM (catalyst coated membrane) bezeichnet. Auf beiden Seiten der MEA wird eine Gasdiffusionslage (GDL), auch "backing layer" oder DM (diffusion media) genannt, angepresst. Die poröse und dadruch Gasdurchlässige GDL besteht häufig aus einem Graphitfasergewebe (0,1 bis 0,3mm) und erfüllt mehrere Aufgaben. Als erstes einmal muss die GDL die beiden Reaktionsgase möglichst optimale verteilt an die gesamte aktive Elektrodenfläche heranführen. Weiterhin muss die GDL die in den Elektroden erzeugte elektrische Ladung (Elektronen) ableiten. Und zusetzt reguliert die GDL den Wasser(dampf)transport weg von der Membran.

Mehr oder weniger komplizierte Kanalstrukturen in den sogenannten Bipolarplatten realisieren die flächige Gaszuführung an die GDL. Die Bezeichnung Bipolarplatte macht deutlich, dass auf den gegenüberliegenden Flächen eine umgekehrte Spannung anliegt. In der Anordnung mehreren Einzelzellen (siehe unten) wird dies deutlicher. Die aus den Bipolarplatten herausgearbeiteten Kanalstrukturen werden also "flow field" bezeichnet.

III. Der PEMFC-Stack

Die von einer Zelle erzeugte Spannung beträgt je nach angeschlossener Last zwischen einem halben und etwa einem Volt (siehe oben). Durch die elektrisch Serienschaltung mehrerer Einzelzellen zu einem sogenannten Stack (Stapel) kann diese Spannung auf einen vernünftigen Wert erhöht werden. Brennstoffzellenstacks bestehen aus fünf (Labormaßstab) bis mehreren Hundert Einzelzellen.

Bei einem bipolaren Stackaufbau stehen Einzelzellen jeweils durch eine gemeinsame Bipolarplatte miteinander in elektrischem Kontakt. Die Bipolarplatte führt auf der einen Seite das Brenngas und auf der anderen Seite Luft oder Sauerstoff zu den jeweiligen Elektroden. Der Name Bipolarplatte kommt durch die an beiden Seiten anliegende Spannung mit unterschiedlichem Vorzeichen: Minuspol an der Anodenseite (Wasserstoff) und Pluspol an der Kathodenseite (Sauerstoff). Die Summe der einzelnen Zellspannungen nennt man Stackspannung. Diese wird durch Stromabnehmer oder Stromsammler an Anfang und an Ende des Zellstapels abgeführt. Der Strom, den der Stack liefert, hängt von der Größe der aktiven Fläche ab. Doppelte Fläche bedeutet doppelter Strom.

III. 1. Leistung eines Brennstoffzellenstacks

Die elektrische und thermische Leistung eines Brennstoffzellenstacks hängt von der Anzahl der Einzelzellen und der Größe der aktiven Fläche (Elektrodenfläche) ab.

Beispiel:
Ein Stack besteht aus N = 100 Einzelzellen mit einer aktiven Fläche von A = 300cm ². Bei einer durchschnittlichen Einzelzellspannung von 650mV und einer Stromdichte von 0,8A/cm² liefert dieser Stack folgende elektrische und thermisch Leistung (in genau diesem Betriebspunkt):

U_Stack = N · U_EZ(j) = 100 · 0,65V = 65V

I_Stack = A · j = 300cm² · 0,8A/cm² = 240A

P_{el, Stack} = U_stack · I_stack = 65V · 240A = 15600W = 15,6kW

P_{therm, Stack} = (N·1,253V - U_Stack) · I_stack = (100·1,253V-65V) · 240A = 14472W = 14,5kW

Bei einer Anodenstöchiometrie von λ_anode = 1,1 und einer Kathodenstöchiometrie von λ _cathode = 2 benötigt dieser Stack nach obigen Gleichungen

0,273 g/s oder 183,8 slpm Wasserstoff und 795,7 slpm Luft

IV. Eigenschaften der PEMFC

Die Eigenschaft eines Brennstoffzellenstacks hängt von einer Vielzahl von Parametern ab. Zum einen von den Eigenschaften der einzelnen Komponenten, aus denen er zusammengesetzt ist. Zum anderen haben die Betriebsparameter, mit denen der Stack gefahren wird, einen entscheidenden Einfluss.

Der optimale Betriebspunkt von Brennstoffzellenstacks wird durch Kennlinien charakterisiert. Dabei wird ein Betriebsparameter variiert, alle anderen Betriebsparameter bleiben unverändert (siehe U-I-Kennlinie weiter oben). Über diese Kennlinien kann dann der geeignete Betriebspunkt gefunden werden.

Unter anderem haben folgende Parameter einen Einfluss auf das Verhalten von Brennstoffzellen:

• Mehrere Firmen entwickeln die Kernkomponente von Brennstoffzellen, den Elektrolyten. Vor allem aber die Forschung und Entwicklung der Membranen und kompletter MEAs für PEMFCs ist noch lange nicht abgeschlossen. Es gibt sehr große Unterschiede in Bezug auf Haltbarkeit, mechanische Stabilität, Stromdichte etc. bei den einzelnen Membranen und MEA´s.
• Die Katalysatorbelegung ist in den letzten Jahren stark gesunken und liegt zur Zeit im Bereich von weniger als 0,5 mg/cm² Edelmetall. Dennoch ist auch die Entwicklung der Katalysatormaterialien noch nicht am Ende angelangt.
• Das Flowfield in den Bipolarplatten hat einen erheblichen Einfluss auf die Leistung der BZ. Die Reaktionsgase sollen möglichst an jeder Stelle und gleichmäßig an der Membran in ausreichendem Maß zur Verfügung stehen.
• Das Wassermanagement spielt bei aktuellen Membranen eine entscheidende Rolle. Die Protonenleitfähigkeit der Membran und damit die Leistung des Stacks steigt proportional zum Wassergehalt der Membran. Deshalb muss die Membran feucht gehalten werden, sie darf nicht austrocknen. Der Wassergehalt der Membran kann zum Beispiel über die Befeuchtung der Reaktionsgase erhöht werden.
  Andererseits darf die Zelle nicht zu feucht werden. Es besteht die Gefahr, dass sich die Kanäle in der GDL mit flüssigem Wasser zusetzen und damit der Gastransport nicht gewährleistet ist.
• Die theoretische Zellspannung nimmt zwar mit zunehmender Zelltemperatur ab, aber die Stackleistung erreicht bei einer bestimmten Temperatur ein Maximum. Dieses liegt im Bereich zwischen 50 und 80°C. Bei höheren Temperaturen ist ein stabiles Wassermanagement schwer zu realisieren.
• Die Art und Reinheit der Reaktionsgase spielen eine große Rolle. Die PEMFC ist sehr empfindlich gegenüber Verunreinigungen des Wasserstoffs, vor allem im Bezug auf gasförmige Schwefelverbindungen und Kohlenmonoxid (CO). Auch wenn eine BZ mit Luft anstatt reinem Sauerstoff betrieben wird führt dies logischer Weise zu großen Leistungseinbusen (geringer Sauerstoff-Partialdruck). Ebenso hat ein erhöhter Druck der Reaktionsgase eine großen Einfluss auf die Leistung.
• und viele, viele mehr!

Quellenangaben siehe Link-Seite.

zurück zu www.pemfc.de

letzte Änderung: 24. Juli 2020, Dr. Alexander Kabza